In this post we are briefly going to discuss two common graph traversal methods, depth-first search (DFS) and breadth-first search (BFS). These are not the only ways to visit all the nodes in a graph in a certain order, but they are two common methods that are useful for many applications [1]. As always, if you are looking for a code implementation, you can find code for both DFS [2-4] and BFS [5].

Depth-first search starts at the root node of the graph (or just some node of the graph chosen at random) and explores each branch of the graph completely before going on to the next branch [6]. We go deep into the tree before moving on to explore other parts, hence depth-first search. Conversely, BFS starts at the root node and then explores all of its immediate neighbors before visiting their children [6]. If you think of a graph as a series of layers, BFS ensures that we completely visit one layer before moving on to the next.

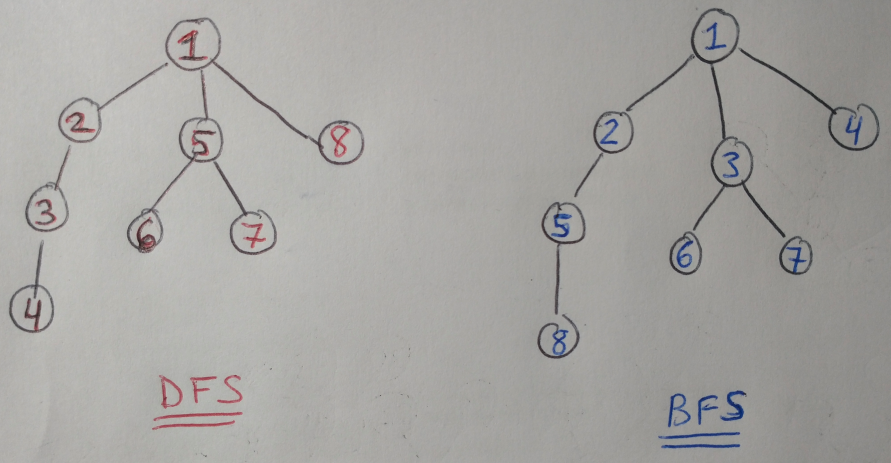
Figure 1

In general, we can use stacks to implement DFS and queues to implement BFS [1]. With the stack, we add the neighbor nodes to our current node, and then pop the node off the top of the stack and repeat the process from that node [1]. This means that we always traverse to the next node that was most recently discovered, which drives us to follow a single branch before moving on to the next branch [1]. Conversely, in BFS, the queue stores the list of immediate neighbors that need to be visited; we visit the nodes that we added to the queue first (i.e. the immediate neighbors of our current node) before moving on to nodes that are farther away in the graph [1].

Breadth-first search is also not implemented recursively, it iterates through the neighbor nodes in the queue [6]. In contrast, DFS can be implemented recursively and does not require use of a queue to keep track of the nodes it needs to visit or has visited [6].

Laakmann McDowell recommends using DFS if our objective is to visit every node in the graph [6]. However, BFS is better if we are looking for the shortest path between two points [6]. Why is this? Imagine that we are looking for the connection between two friends in a large social network of all the people living in a city [6]. We will find the connection between the first friend and the second friend more quickly if we stay close to the first friend in the network for as long as possible [6]. If we were to use DFS, we would quickly move away from the first friend, and also possibly not get any closer to the second friend if we picked the wrong branch [6].

In fact, a variation of this approach is called bidirectional search, which finds the shortest path between two nodes by running two BFS calls simultaneously from each of the two nodes [6]. When the two searches collide, we have found our shortest path between the nodes [6].

References:

[1] Kingsford, C. and Ma, J. “DFS and BFS implementations.” 15-351/15-650/02-613 Algorithms and Advanced Data Structures, Fall 2020.

[2] “How to implement depth-first search in Python.” Edpresso. https://www.educative.io/edpresso/how-to-implement-depth-first-search-in-python Visited 26 Jan 2021.

[3] Ebrahim, M. “Depth First Search algorithm in Python.” Like Geeks. 01 July 2020. https://likegeeks.com/depth-first-search-in-python/ Visited 26 Jan 2021.

[4] Mann, E. “Depth-First Search and Breadth-First Search in Python.” 05 Mar 2014. https://eddmann.com/posts/depth-first-search-and-breadth-first-search-in-python/ Visited 26 Jan 2021.

[5] “How to implement a breadth-first search in Python.” Edpresso. https://www.educative.io/edpresso/how-to-implement-a-breadth-first-search-in-python Visited 26 Jan 2021.

[6] Laakmann McDowell, G. Cracking the Coding Interview, 6th edition. 2016. CareerCup, LLC.