While working on my post about hash tables, I came across the concept of dynamically resized arrays/lists, which I didn’t know anything about. I wanted to write a post specifically about how we can resize arrays or lists because I think the details are useful to know when discussing more complex data structures. Many thanks to Yasufumi Taniguchi’s excellent article for guiding this post [1]. We will first talk about where dynamically resized arrays and lists come into play and some factors to consider when resizing them, then we will get into some of the details of how efficient resizing can be.

What Factors to Consider in Dynamic Resizing?

Some programming languages allow you to create data structures like lists and arrays that will automatically grow as you add items [2]. (Sometimes, though, you have to declare the size of the structure at the start and you cannot exceed that capacity once that instance has been created [2].) For example, if we create a list in Python, we can continuously append or remove items from the list without explicitly managing the size of the list - Python will do that for us in the background [1]. Resizing simply means that as the list changes in size - for example, as we append more elements - the list is copied to a new, larger list with more room for additional entries [1].

One typical approach to resizing is to double the size of the list once the list is full [2]. The doubling of the list can take time and additional space, but the idea is that it happens infrequently enough that the list is still a fairly efficient data structure (both in terms of time and space) [2].

In fact, there are some factors to balance to ensure that this is true - that the dynamically resized list is an efficient structure [1]. For example, we have to decide how much to expand the list by - if we add too little memory, then we will waste time on performing the resizing operation too frequently [1]. If we add too much memory, then we will be space inefficient [1]. Similarly, when we need to reduce the size of the list, how much of a space reduction should we make? Too little reduction means that we’re going to continue wasting memory even after the resizing is performed [1]. Too much of a space reduction means that we will then need to perform many costly resizings later when we add elements back into the list [1].

We can describe how much we we increase or decrease the size of the list with each dynamic resizing by a resizing factor k [1-2]. Different languages use different values for k (Python has k = 1.125, Java has k = 2) but in general, k is greater than 1 and so resizing (or reallocation) will create an array that is k times as big as the previous array [1].

Now that we have some basic intuition about how resizing a list or array works, let’s look at the specific details of the implementation.

Time Complexity of Resizing Arrays and Lists

Let’s say that we have a list with a resizing factor k = 2 - that is, every time we resize the list, it either doubles or halves in size (depending on if we are appending or removing elements). Remember that every time we change the size of the list, we have to copy it to a new list, and it takes O(1) time to copy one element. So let’s see what happens as we add items to a list that begins as size 2, with one element contained within it [1]:

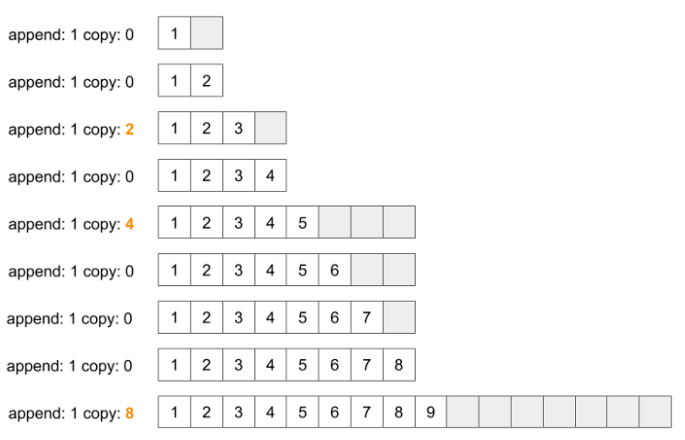
Figure 1 - Source [1]

As you can see in Figure 1, we have to copy the list over several times as we keep adding elements to it [1]. Every time we copy, it takes O(n) time where n is the number of items in the list. In total, we can write the time complexity of adding n items as [1]:

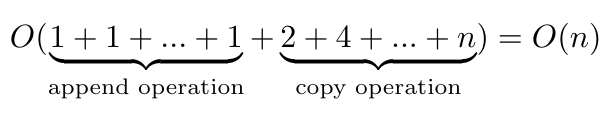
Equation 1

Essentially we can ignore the constant terms and reduce this to see that the time complexity of resizing a list or array is O(n) [1-2].

But the amortized runtime of resizing a list is only O(1) [2]. Why is that? Let’s imagine that we have a list of size N and we are going to work backwards to see how many elements we have copied at each resizing event [2]. We will assume that k = 2 so that if the list is size x, before the resizing it was size x/2 and so x/2 elements had to be copied over to the new list of size x [2]:

Final capacity increase: N/2 elements copied

Previous capacity increase: N/4 elements copied

Previous capacity increase: N/8 elements copied

…

Second capacity increase: 2 elements copied

First capacity increase: 1 element copied

Now let’s add up the total number of copies that we had to make to insert N elements into the list [2]:

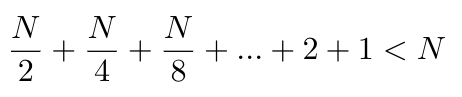
Equation 2

Why is the sum less than N? Laakmann McDowell suggests thinking of it as the distance you need to walk from your house to the grocery store. If you walk half of that distance, and then half of the remaining distance, and then half again, you will almost, but never quite reach the grocery store (i.e. you will almost, but never quite reach N) [2]. So the total number of insertions to the list takes O(n) time, although in general the insertion can be done in constant time because we are amortizing the cost over multiple resizing operations [2]. The worst case runtime is O(n) [2].

I hope that explanation was helpful. This is something to consider when creating more complex data structures that will rely on lists or arrays that dynamically resize, because the resizing could take significant time, as we have seen here.

References:

[1] Taniguchi, Y. “What You Should Know about the Python List.” Medium. 14 Jan 2019. https://medium.com/@yasufumy/data-structure-dynamic-array-3370cd7088ec Visited 16 Jan 2021.

[2] Laakmann McDowell, G. Cracking the Coding Interview, 6th edition. 2016. CareerCup, LLC.