This is the 3rd post in my series on solving controller design problems from Nise [1]. This time we are going to design a pure derivative controller to meet a settling time requirement. The interesting part of this problem is how we used the settling time requirement to choose the controller zero’s location.

Example 9.3: Designing an Ideal Derivative Controller [1]

In this problem we are given a plant and told to design a derivative controller that reduces the settling time by a factor of 3. We are also told that the plant has 16% overshoot (we will assume this is fixed throughout the problem). The solution flow is:

(1) Draw out the root locus.

(2) Calculate the damping from the overshoot specification. Use the damping coefficient to find the closed loop pole locations.

(3) Use the pole locations to solve for the uncompensated settling time of the system. Also calculate the desired compensated settling time (reduce by a factor of 3).

(4) Choose the location of the new compensated closed loop poles by calculating real and imaginary components from the settling time requirement.

(5) Use the sum of the phase contributions from all open loop poles and zeros to choose the position of the controller zero.

Figure 1

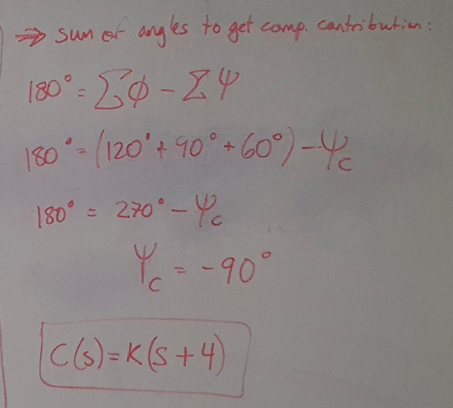Figure 2

References:

[1] Nise, Norman S. Control Systems Engineering, 4th Ed. John Wiley & Sons, Inc. 2004.