In this post, I am going to introduce the basics of neural networks, because they are fundamentally useful tools in reinforcement learning (RL). If you recall from my earlier post, deep RL uses neural networks as “function approximators” for the Q-function in reinforcement learning. The Q function can be very complex so we need to use something like a neural network to represent it. (In fact, we use neural networks to represent many different complex functions, not just the Q function, although it is a good first example.) In this post we will discuss the architecture of a neural network, some of the mathematics used to make it work, and different flavors of neural networks as well as their applications. It is likely that this post will lead to several others because there is a lot of material to cover!

Let’s begin with the inspiration for neural networks. As their name suggests, neural networks (NNs) are based on the structure of the human brain. A good illustration of this is shown in the figure below, where we see that structures and their functions in the human brain have analogous components in the architecture of a NN. For example, the human brain is made up of neurons (diagram A) which is made up of a cell body, dendrites and axons [1]. I am not sure whether we explicitly refer to the dendrites and axons when discussing NNs, but I have read articles that reference “cells” when discussing the functions of specific neurons in a NN [2]. The human neuron is equivalent to a “unit of calculation,” i.e. a single function or a single node in a NN (diagram B) [1]. In a human brain, neurons communicate with each other via synapses (diagram C), and the NN equivalent is to use weighted values to transfer data from one node in the network to another (diagram D) [1]. So a neural network is essentially a brain, where many (~millions) of nodes are each performing a single calculation and together the neurons are learning to complete complex tasks.

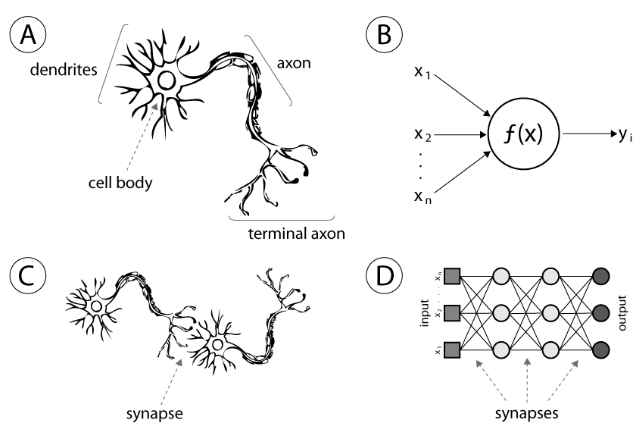
Figure 1 (Source [1])

In a neural network, the neurons are perhaps more organized than in the human brain, because they are arranged in layers [1]. Any NN containing more than 3 layers is considered a deep NN (hence they turn reinforcement learning into deep reinforcement learning) [1]. The input layer takes in data and performs calculations on it. The output of that layer is passed as input to the next layer via weights (represented as lines in Figure 1, diagram D above). All intermediate layers are called hidden layers, and eventually the output layer returns the final result [1].

How is it possible that all these individual neurons performing one mathematical operation can give rise to artificial intelligence behavior? In his tutorial, which I will describe in more depth in another post, Karpathy builds a neural network and looks under the hood to show us what some of the specific neurons in the network are doing [2]. In his example (the NN is trying to learn to replicate text like Shakespeare or Wikipedia markdown), one specific neuron is active when it sees URLs in markdown [2]. Another neuron is active when it sees the end of a line of text [2]. These neurons have each specialized in identifying one specific pattern, and the information they pass to the rest of the network tells the network when it needs to write the “http://” sequence or when it needs to start a new line [2]. If we imagine thousands of nodes all looking for very specific patterns, then we can imagine that the network in its entirety can notice many things about a text and replicate it appropriately [2].

Neural networks are not new concepts - most researchers identify their origins in the concept of perceptrons from the 1960s, specifically multilayered perceptrons [1]. But NNs have seen a resurgence of popularity in recent years because we now have the hardware necessary to be able to run in them in a feasible amount of time [1]. (In his tutorial, Karpathy demonstrates the functionality of a NN made up of 2 layers of 512 neurons which requires tuning of approximately 3.5 million independent parameters, and yet he writes that one training iteration takes 0.46 seconds to process on a GPU [2]!) Early research into perceptrons and neural networks did not favor using multiple hidden layers - if a researcher wanted to improve the function approximation provided by the NN, they simply added more neurons to each layer [1]. But these early researchers did not realize that limiting themselves to a single hidden layer essentially meant that they were limited to creating a linear mapping between the input and output layer [1]. It is only possible to create a more complex, nonlinear function approximation when using multiple hidden layers, which is why those are gaining in popularity in today’s research [1].

In a subsequent post, I will discuss in detail how the neural network operates on data, but for now I will give a brief overview. Neural networks follow two steps for every iteration through the network [3]. First, they use forward-propagation to take in the input data and produce an output [3]. Secondly, they will compare the output to the actual value they should have calculated (as provided by the training data) [3]. There will be some error between the actual and predicted values, and so the neural network will back-propagate the error through the neural network [3]. The process of backpropagation updates the weights in all the links so that the nodes which contributed the most to the error are penalized [3]. The ultimate goal of the neural network is to reduce the error between the outputs that it calculates and the actual values from the training data [3]. We will go into this in more detail in the next post.

References:

[1] Aaron. “Everything You Need to Know about Artificial Neural Networks.” Josh.ai on Medium. 28 Dec 2015. https://medium.com/technology-invention-and-more/everything-you-need-to-know-about-artificial-neural-networks-57fac18245a1 Visited 13 Dec 2019.

[2] Karpathy, Andrej. “The Unreasonable Effectiveness of Recurrent Neural Networks.” 21 May 2015. http://karpathy.github.io/2015/05/21/rnn-effectiveness/ Visited 16 Dec 2019.

[3] Al-Masri, A. “How Does Back-Propagation in Artificial Neural Networks Work?” Towards Data Science on Medium. 29 Jan 2019. https://towardsdatascience.com/how-does-back-propagation-in-artificial-neural-networks-work-c7cad873ea7 Visited 28 Mar 2020.