In my last post we introduced neural networks, and in today’s post I would like to explain how neural networks “learn” by giving an overview of the learning algorithm. Neural networks learn by iteratively trying to recreate an output, given some inputs, by comparing the output that it generates to the desired value. The difference between the neural network’s output and the desired value can be used to calculate the error for a given learning iteration. The neural network uses the error to update the weights on each node in order to reduce that error on the next iteration. Over many iterations, the neural network can learn to complete the assigned task with a high degree of accuracy. Let’s dive in to understand how the learning process works.

Problem

Let’s say that we want to train our neural network to learn to do binary classification - basically we want it to do the same task that we can perform using linear regression or logistic regression. We are going to construct a neural network and give it a set of training data to learn to perform this task. Then we will present the neural network with some new data that it has never seen before, and see how successfully it classifies this new data.

An overview of a neural network and its learning process is shown in Figure 1 below.

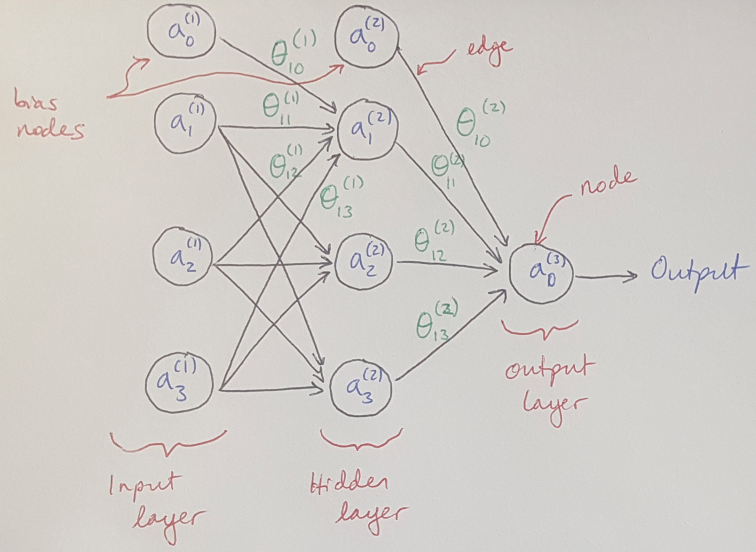
Figure 1 - Inspired by [3]

Setup

Our neural network will have a series of nodes arranged into 3 layers: the input layer, the hidden layer in the middle, and the output layer (see Figure 1) [1]. We can choose how many nodes we want to put into the middle layer - more nodes allow us to fit our model to more complex functions, but they will also come at a higher computational cost [2]. Having more nodes will also make it more likely that we will overfit* our model to the data [2].

Each layer of nodes will take in information from the previous layer as a weighted sum. This sum will be fed into the nodes’ activation functions, which determines whether or not each node should “fire” and send information to the next layer. This process is repeated in every layer until the final answer is returned by the output layer. The neural network then calculates the error between the output and the training data, and uses that information to adjust the weights in the neural network via backpropagation [1,2].

Weighted Sum of Inputs

We define a weighted sum that generates the input to the activation function. In this example, theta represents the weights along each edge in the neural network (see Figure 1) and a represents the output from the previous layer [3]:

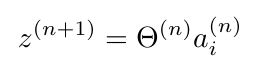
Equation 1

The index i denotes the i-th node in a layer, and n denotes the layer that the value corresponds to. Notice that each layer may contain nodes that are not connected to earlier layers. These are called bias nodes [2, 3].

Activation Function

Each node needs an activation function [1]. The activation function is a mathematical expression that defines the output of a node [4]. The activation function decides if a particular neuron should be “fired” to help the neural network produce the correct output [4]. Some popular activation functions include tanh, the sigmoid function or rectified linear units (ReLUs)** [2]. Notice that all of these functions share the property that their derivatives involve the original function [2]. This is useful because we will need to calculate their derivatives during backpropagation (more information below) [2]. For example, the derivative of tanh is:

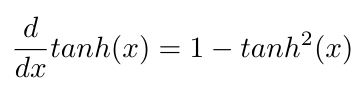
Equation 2

Notice that the derivative uses tanh. This is helpful because if we calculate tanh once, we can re-use that value to calculate the derivative, which speeds up computation time [2]. We will use tanh as our activation function for our hidden (middle) layer:

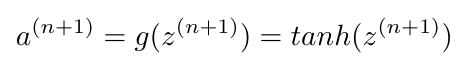
Equation 3

We are going to use a different activation function for the output layer, because we want it to return a probability [2]. We will use the softmax function to generate these probabilities [2]. The softmax function is able to convert a vector of values that may contain negative numbers and numbers greater than 1 into a vector of values that all lie in the range (0, 1) [6]. This means that each of these converted values now represents a probability that corresponds to the size of their initial values (i.e. bigger values have bigger probabilities) [6]. The softmax function is frequently used with neural networks to return a probability distribution for all the output values over the possible output classes [6].

Error Calculation and Backpropagation

We will compare the output from the neural network to the known value in the training data, and calculate the error between these two values. That information will be passed back through the network via backpropagation to update all of the weights, theta, so that the network returns a closer value on the next iteration. Backpropagation is a complex process in its own right, so I will write a separate post to explain it in detail.

*Overfitting is caused when the model tries to fit to absolutely every data point in the training set [3]. As an example, if you are trying to learn the difference between two categories, a model that is overfit to the data might draw a decision boundary that contorts itself to match the given training data, but will give poor results on new data [3]. See the figure below for more illustration.

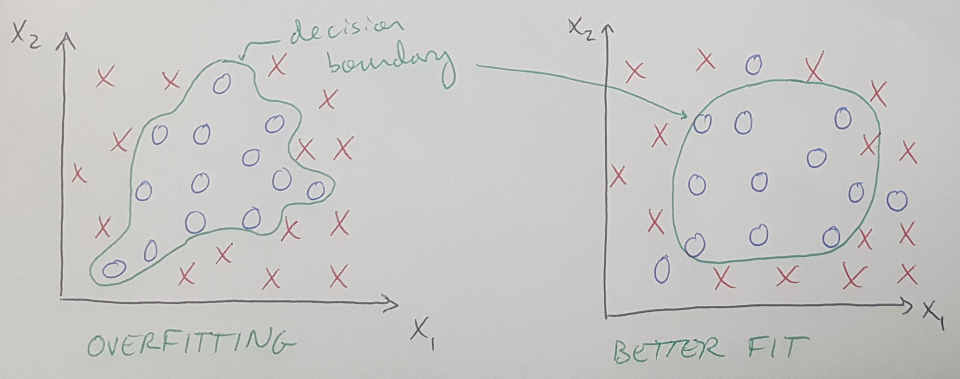
Figure 2

**The rectified linear unit is also a ramp function, and a plot of the function is shown below [5]. It was developed relatively recently, in 2000, and was first used in neural networks in 2011, and was shown to have better performance than neural networks that used the sigmoid function [5].

Figure 3

References:

[1] Al-Masri, A. “How Does Back-Propagation in Artificial Neural Networks Work?” Towards Data Science on Medium. 29 Jan 2019. https://towardsdatascience.com/how-does-back-propagation-in-artificial-neural-networks-work-c7cad873ea7 Visited 28 Mar 2020.

[2] Britz, D. “Implementing a Neural Network from Scratch in Python – An Introduction.” 03 Sept 2015. http://www.wildml.com/2015/09/implementing-a-neural-network-from-scratch/ Visited 09 Apr 2020.

[3] Ng, A. Machine Learning course, week 4 lecture notes on neural networks. https://www.coursera.org/learn/machine-learning/supplement/jtFHI/lecture-slides Visited 15 Apr 2020.

[4] missinglink.ai. “7 Types of Neural Network Activation Functions: How to Choose?” https://missinglink.ai/guides/neural-network-concepts/7-types-neural-network-activation-functions-right/ Visited 06 Apr 2020.

[5] Wikipedia. “Rectifier (neural networks).” https://en.wikipedia.org/wiki/Rectifier_(neural_networks) Visited 09 Apr 2020.

[6] Wikipedia. “Softmax function.” https://en.wikipedia.org/wiki/Softmax_function Visited 09 Apr 2020.